視覚やほかの感覚様相の感覚閾に関する知識は、感覚器官がどのように構成されているかという基本を理解する上で重要である。たとえば目の中の光を感知できる色素の一分子が光の単一の光子に反応するという知識は、光を感知できる色素がどのように働くかを理解する上で重要な手がかりとなる。
しかしながら、私たちの日常の視覚行動はほとんどが閾より上のまたは閾値以上の条件(suprathreshold:suprathreshold conditions)という状況で行われる。19世紀半ばに生理学者エレンストン・ハインリッヒー・ウェバー(Ernst Heinrich weber)と物理学者ギュスターブ・フェヒナー(Gustav Fechner)から始まり、科学者たちは、さまざまな強度の刺激を人間に提示し、刺激に対する反応の大きさの測定を試みることによって、閾以上の刺激強度と対応する感覚の大きさとの関係を研究してきた。
次のような実験を想像してみる。薄暗い部屋で腰をおろしてスクリーンを見ている。一連の試行のそれぞれにおいては、小さな光点がスクリーン上に現れる。その光点は、物理強度が試行ごとに異なる。あなたのしごとは、その試行の光点がどのくらい強く見えたかを反映する一つの数を試行ごとに割り当てることである。
それで、非常に薄暗い光に対しては1を割り当て、非常に明るい光に対しては100を割り当てるかもしれない。
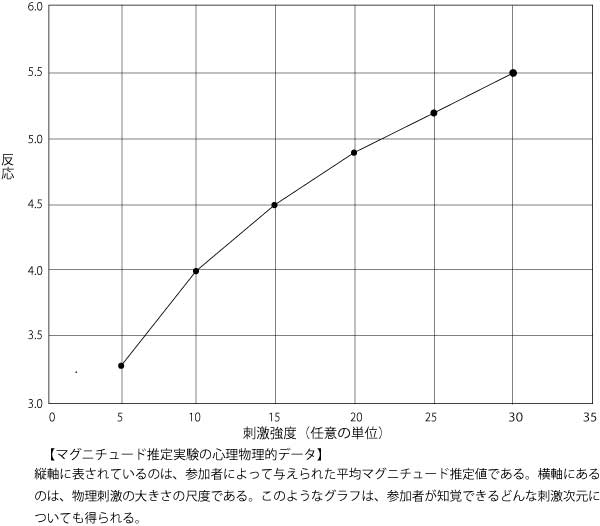
表はこのような実験の典型的なデータを示している。
20世紀半ばには、アメリカの心理学者スティーヴンス(S.S.Stevens)が、この種の実験を用いて閾値以上の感覚に関する集中的な研究を実施した。彼はデータを解釈して、二つの仮定から、彼の名前の付いた一つの法則を導いた。一つめ仮定は、「マグニチュード推定実験の心理物理的データ」でのウェーバー-フェヒナーの法則が正しいということである。
すなわち、標準刺激より上のところの丁度可知差異は、その標準の一定の割合だということである。二つめ仮定は、(距離がメートルでうまく測定され、重さがグラムでうまく測定されるように)、心理的強度が丁度可知差異の単位でうまく測定されるということである。
これは、たとえば4jndと7jndとの差(すなわち3jnd)が参加者にとっては10jndと13jndとの差(同様に3jnd)と同じだということを意味する。結論を言えば、すなわち、スティーヴンスの法則とは、先の二つの仮定に含まれているが、知覚された心理的大きさ(Ψ)が物理的大きさ(Φ)のベキ関数(power function)だということである。
その意味は、ΨとΦの関係は(基本的に)Ψ=Φrだということである。ここでrは、各感覚様相に固有の指数(ベキ関数の)(exponent(of power function))である。表に示されている関数は、指数が0.5のベキ関数である。(これは、ΨがΦの平方根に等しいことを意味する)。
スティーヴンスらは、物理的強度と心理的強度の関係がベキ関数であるという命題を支持する実験を文字通り数千も報告している。
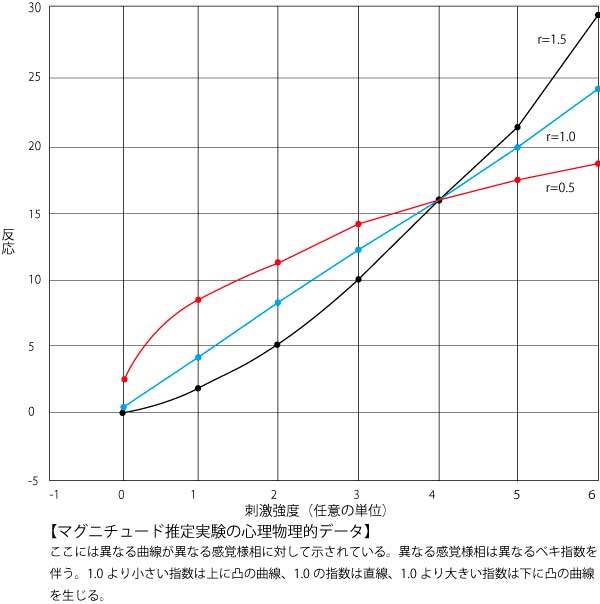
この表で示されているように、指数が1より小さいベキ関数は、音の大きさに対応する関数のように、上に凸である。すなわち、物理的強度の水準増大は、感覚における反応が次第に小さくなる結果となる。対照的に、指数が1より大きいベキ関数は、電気ショックに対応する関数のように、下に凸である。すなわち、物理的強度の水準増大は、感覚における反応が次第に大きくなる結果となる。
なぜ指数が感覚様相間で異なるのか、正確な理由は知られていない。しかしながら、光の強度のような比較的害のない感覚様相は指数が1より小さく、電気ショックのような比較的有害な感覚様相は、指数が1より大きいことに気がつくとおもしろい。
こういった状況は、おそらく適応的な目的を果たしているのであろう。光の強度のような比較的「害のない」感覚様相の場合には、物理的強度と心理的反応の関係は、単に、すぐに問題となるかもしれないし、ならないかもしれないような、有益な情報を伝えるだけである。
たとえば、騒々しい汽笛はすぐ近くの列車を予告し、列車が離れていることを示すより静かな汽笛よりももっと注意を払う必要があることを合図する。しかしながら、痛みのような様相は、即座に行為の必要性を合図する。身体への危害ありそうだから、即時の行為がなされるべきだ、ということを知覚者にできるだけ明瞭にすることは意味があるであろう。
もし、誤って指がまっかに焼けた石炭に触れたなら、こういった非常に強い痛みを引き起こす刺激が、非常に大きい反応を生み出すことは重要である。さもなければ、生命や手足を失うこともあり得るからである。
信号検出論
感覚系の仕事は一見単純なことのように見えるかもしれない。すなわち、もしも何か重要なものが存在すれば、たとえば肺に悪性腫瘍があれば、それを診た医者が可能な治療法を考える、というような適切な行動を起こせるように、提供される感覚情報を通じてその存在を記録せよ、というような仕事である。
しかしながら、実際には人生はそれほど単純ではない。なぜならば、通信工学者が教えてくれるように、いかなる種類の情報も信号(signal)と雑音(noise)からなるからである。(「通りの向かいのあのパーティーから、ものすごくたくさんの不愉快な雑音が聞こえてくる」という場合のように)普通の言葉では聴覚領域のみに関係する「ノイズ」という用語に惑わされないでほしい。
一方、科学の世界では、「信号」は情報の重要な関連部分のことを言い、「雑音」は情報の重要でない部分のことを言う。後に視覚様相のところで実例を挙げるが、雑音はどんな種類の情報でも部分として生じる。決定的なのは、どの様相においても、検出器の仕事が、信号をぼかしたり隠したりすることのできる雑音から、必要つする信号を取りだすことだということである。
この問題を現実の場面で例証するために、アメリカの医療過誤訴訟を述べることにする。放射医療であるA医師が、日常的な診察の間に、患者であるP氏の胸部レントゲン写真を調べた。不幸にも、P氏の胸部には小さいが癌のような腫瘍があったのだが、A医師によって検出されず、3年後かなり大きくなって結果的にP氏の死を招いた。
P氏の家族は、A医師に対して訴訟を起こし、腫瘍は最初のレントゲン写真で検出可能であったし、A医師は検出していたはずだと主張した。次の裁判の間に、P氏の家族は、もう一人の放射医師であるB医師に、専門家として参考人を依頼した。
B医師は初めてに、準備の一環として、P氏の死の直前に撮られた最近のレントゲン写真を見た。そこには、その辞典では大きな不吉な腫瘍がはっきりと見えた。B医師は次に、A医師が見た最初のレントゲン写真を見て、A医師が見落とした、当時はもっと小さかった腫瘍を容易に「見つけた」。B医師の結論は、自分が最初のレントゲン写真の中に腫瘍を見つけることができたのだからA医師も検出していたはずであり、それゆえA医師はそれを見落とすほど不注意だったというものであった。
この事例は、感覚と知覚における興味深い問題をいくつか提起する。ここでは、感覚(sensation)とバイアス(bias)の区別という問題に焦点を合わせる。この区別を理解するために、レントゲン写真が正常なのかそれとも腫瘍の存在を示しているのかを決定しようとしてレントゲン写真を見ている放射線医の課題を一般的に考えてみよう。
科学の言葉では、この課題は先述にあるように、雑音に埋め込まれた信号を検出しようとする課題である。この概念は下に図解されている。図は背景が三つとも同じであり、任意の視覚的ノイズからなる。課題は、このノイズのどこかに埋め込まれた、黒くて小さなシミのようなものが存在するか否か、を決定することであると仮定する。

この課題は、レントゲン写真の中に輪郭のはっきりとしない腫瘍を見つける放射線医の課題ときわめて類似している。
ヒットと誤警報(hits and false alarms)
さて、上図のような一連の刺激全体が与えられたと仮定する。左のパネルのようにノイズしか含まない刺激もあるし、右のパネルのようにノイズと信号を含む刺激もある。あなたの課題は、信号を含む刺激には「はい」と答えることである。重要なことは、この課題を完璧に実行するのは不可能だということである。
理由は、この左のパネルにはノイズしか含まれない。あなたは、このパネルを念入りに調べるや否や、信号が含まれていると思うかもしれない。たとえば、矢印が示している領域で、捜している黒いシミのようなものに似た領域である。それで、あなたは、当然ながら、それに対して「はい」と応答するかもしれないが、この場合は正しくない。
もしそうしたら、あなたは誤警報(false alarm)と呼ばれる誤りをおかしたことになる。
いま描写したたぐいの信号検出実験では、正しくない「はい応答」を生じたノイズのみの試行の割合を測定することができる。この比率は誤警報率(false-alarm rate)と呼ばれる。私たちはまた、正しい「はい」応答を生じた、ノイズと信号の試行の割合をすることもできる。そのような応答は、ヒット率(hit rate)と呼ばれる。
私たちはいまや感覚器官の感度を研究するための強力な道具を手にしている。検出すべき信号が全く存在しなくても、誤警報率に等しい確率で参加者が「はい」と答える。ヒット率が誤警報率を超えた条件下でのみ参加者が信号を検出したと推論する。もしヒット率が誤警報率を大きく超えたら、感度が高いと推論し、ヒット率が誤警報率を少ししか越えなければ、感度が低いと推論し、ヒット率が誤警報率に等しければ、感度がゼロであると推論する。
感受性とバイアス
ここで興味深いのは、参加者は、誤警報率をどのくらいにするかを自由に決めてもよいのである。シャーロットとリンダという仮説上の二人の参加者を想像してほしい。二人とも信号検出が得意であるが、二人は重要な一点において違いがあるとする。
シャーロットは、「用心深い」参加者で、とりわけ信号が存在すると主張するためにはたくさんの証拠を必要とする。シャーロットはめったに「はい」と答えない。これは、誤警報確立が低いがヒット率もまた低いことを意味する。対照的にリンダは「厳格でない参加者」だとする。
リンダは、信号の証拠がわずかでもあると「信号」の存在を主張する。言い換えれば、頻繁に「はい」と答える。これは、彼女の誤警報率を高くするがヒット率もまた高くすることになる。
信号検出分析の最も有益な特徴は、バイアス(bias:βで表される)と感度(sensi-tivity:d’で表される。発音は「ディー・プライム」)の分離を可能にすることである。先ほどの例では、シャーロットとリンダは、バイアス値はまったく異なるが感度は等しいということになる。
前に述べた医療過誤訴訟の件に戻って議論すると、参加者がA医師とB医師の二人いることに注意してほしい。訴訟は、A医師はB医師に比べて感度すなわち腫瘍を検出する能力が劣ると申し立てる。そしてA医師が不注意だったと申し立てられているのは、つまるところこのためである。
しかしながらいまでは、この結論が必ずしも、A医師が最初の腫瘍を検出せず、B医師が検出したという事実から出てこないことがわかる。B医師が単にA医師よりも「はい、腫瘍を検出しました」と答えるバイアスが高かっただけということも同様にあり得るからである。
この後者の説明は、実際、十分理にかなっている。心理学者は、信号検出状況において、期待(expectation)を含むたくさんの要因がバイアスに影響することを発見している。すなわち、信号が存在するだろう、という参加者の期待が大きければ大きいほど、「はい」と応答する参加者のバイアスが大きいのはまったく当然である。
そしてもちろん、B医師には腫瘍の存在を期待するに足る十分な理由があったのであり、一方、A医師には腫瘍の存在を期待する理由はごくわずかしかなかったのである。


コメント