視覚とともに聴覚は、環境に関する情報を得る主要な手段である。聴覚が生じるのは音圧の小さな変化が内耳の膜組織を前後に動かすことができるからである。
音波
音は、風が木の枝の間を勢いよく吹き抜けるときのように、物体の運動や振動から生じる。何かが動くと、その前の空気の分子も共に押される。押された分子は、ほかの分子を押してから、元の位置の戻る。このようにして、圧力変化の波(音波)が空気中を伝わることになる。
この波は、石を池に投げ入れることよって引き起こされるさざ波に似ている。音波は、時間と関数としての空気圧のグラフによって記述できる。一つの種類の音の圧力対時間グラフが図1に示されている。
正弦波を描いた図で、正弦波に対応する音は純音と呼ばれる。音叉が振動すると純音を生み出す。純音は、連続する空気圧縮波からなり、空気圧縮波は正弦波の様相をなす。波の振動は波の強度に対応する。一方、一秒あたりの波の数が周波数である。フーリエ解析と呼ばれる手法を使えば、どんな任意の音波も、周波数と強度の異なる正弦波の和に分解できる。
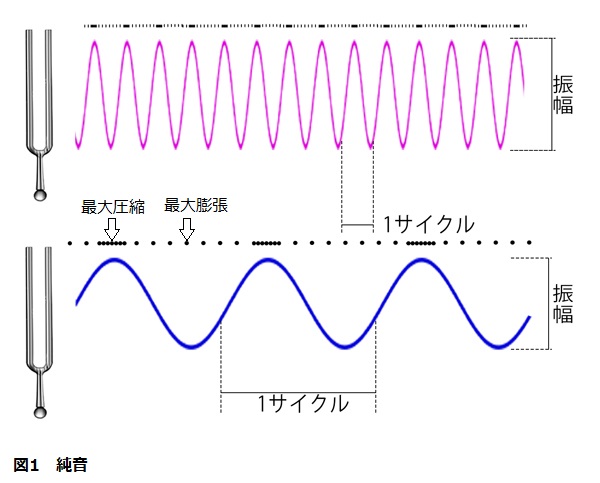
この純音の一つの重要な次元は、純音の周波数(frequency)である。これは、分子が前後に動く1秒あたりのサイクルの数(またはヘルツ)のことである。周波数は音の高さ(pitch)に関する知覚の基礎であり、音の最も際立つ性質の一つである。
高周波数音は、高周波正弦波の形をとり、一方低周波数音は低周波数音波の形をとる。正弦波は聴覚の分析において重要である。なぜなら、フランスの数学者であるフーリエによって証明されたように、どんな複合音も周波数の異なる一連の正弦波の重みづけられた和として表現できるからである。
純音の二つ目の側面は、振幅(amplitude)である。振幅とは、圧力対時間グラフにおける山と谷の間の圧力の差である。音の振幅は、音の大きさ(loudness)に関する感覚の基礎である。音の振幅は、ふつう、対数尺度の一種であるデシベルで記載される。
10デシベルの増加は、その音の閾値以上のところで振幅の10倍の増加に対応する。20デシベルは100倍の増加、30デシベルは1000倍の増加、等々である。100デシベルまたはそれ以上の騒音に絶えずさらし続けられると、永続的な聴力損失は避けられない。
音の最後の側面は、音色(timbre)である。音色とは、音の複雑さに関する私たちの経験のことを言う。私たちが毎日聞く音はほとんどどれも、これまで論じてきた純音ほど単純ではない(例外は音叉といくつかの電子楽器である)。アコースティック学区や自動車や人間の声やほかの動物や滝などによって生み出される音は、音圧の複雑な様相によって特徴づけられる。
音色の違いとは、たとえば、バイオリンによって生み出される中央ハの音を、トロンボーンによって生み出される中央ハの音とは異なったように聴こえさせるもののことである。


コメント